| Код | 478179 | ||
| Дата создания | 2021 | ||
| Страниц | 49 ( 14 шрифт, полуторный интервал ) | ||
| Источников | 9 | ||
| Изображений | 14 | ||
| Оригинальность | 86.7 % | Antiplagiat [ проверено 13.02.2023 ] | ||
|
Файлы
|
|||
|
Без ожидания: файлы доступны для скачивания сразу после оплаты.
Ручная проверка: файлы открываются и полностью соответствуют описанию. Документ оформлен в соответствии с требованиями ГОСТ.
|
|||
К исследованию предлагается привод механизма, содержащий упруго-диссипативный элемент – ременную передачу. При переменной внешней нагрузке в системе возникают упругие крутильные колебания, величину которых следует оценить. В разделе виброзащиты объекта от вынужденных колебаний рассчитываются параметры виброизоляции машины на упругом основании.
1 Краткие сведения о колебаниях системы с одной степенью свободы
Представим машину (машинный агрегат), находящуюся на упругой подвеске под действием гармонической вынуждающей силы F(t) = F0 cos ωt, в виде модели, состоящей из массы m, покоящейся на упруго-диссипативном элементе с характеристиками с и λ. Процедуру определения частотных и диссипативных характеристик машины проиллюстрируем на примере простейшей динамической модели с одной степенью свободы – Н = 1 (рис. 1). При записи дифференциального уравнения удобно воспользоваться непосредственно вторым законом Ньютона:
...
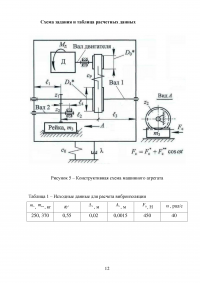
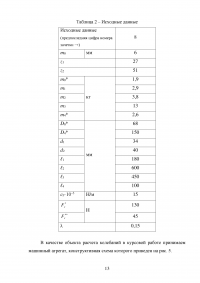
Таблица 1 – Исходные данные для расчета виброизоляции
...
Таблица 2 – Исходные данные
...
2.1 Составление динамической модели привода машины
Рассмотрим расчетную схему привода машины, изображенную в задании, включающую в себя ременную и зубчатые передачи (в т. ч. реечную).
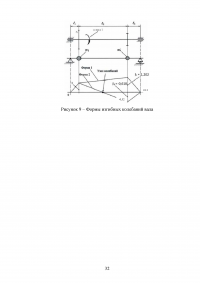
В соответствии с рекомендациями составим динамическую модель привода машины (рис. 6), выделяя лишь наиболее массивные элементы, отображенные сосредоточенными массами (моментами инерции), соединенными между собой кинематическими аналогами и упругодиссипативными связями наиболее податливых элементов. Инерционные и упругие свойства остальных элементов учтем в виде некоторых их приведенных характеристик.
...
2.5 Составление математической модели (ММ) крутильных колебаний элементов привода машины
Составление системы дифференциальных уравнений проведем на базе уравнения Лагранжа второго рода. Уравнение Лагранжа второго рода – математическая модель (ММ) механизма – (в независимых координатах) имеет вид
...
3.1 Определение собственных частот и коэффициентов формы, проверка низшей частоты с помощью метода Данкерлея
Рассмотрим изгибные колебания балки (вала) в одной из плоскостей (горизонтальной или вертикальной) и перейдем сначала к безинерционному упругому «скелету» этой балки. Для этого к связи (безмассовой упругой балке) кроме внешних вынуждающих сил F3 и F4 приложим в соответствии с принципом Даламбера силы инерции (〖-m〗_3 y ̈_3) и (〖-m〗_4 y ̈_4), где y3 и y4 – прогибы под соответствующими массами m3 и m4. Весь расчет основан на решении частотного уравнения для примера балки, представленной на рис. 7.
...
3.2 Низшая частота по методу Данкерлея и коэффициенты формы
Определение низшей частоты по методу Данкерлея – это вычисление приближенного значения первого (низшего) действительного корня частотного уравнения высокого порядка (12). Обычно каждая из последующих частот численно существенно превосходит предыдущую, поэтому приближенное значение меньшего корня (частоты) определим из выражения
...
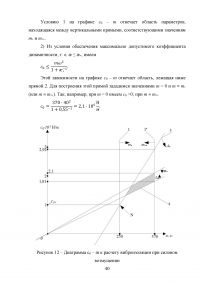
5 Виброизоляция машины на упругом основании. Построение диаграммы с0 – m.
При работе любой машины из-за воздействия внешних сил и неуравновешенности инерционных нагрузок возникают периодические силы, передающиеся на несущие конструкции и корпус машины. При жестком закреплении машины на фундаменте на него полностью будут передаваться силы, возникающие от работающей машины. Частично исключить это явление может виброзащита машины. Она может быть реализована несколькими способами.
...
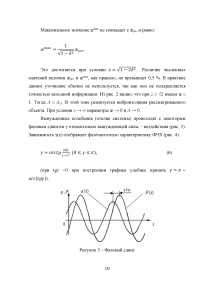
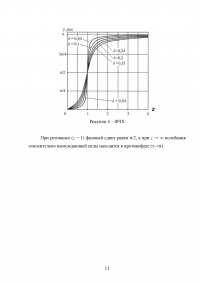
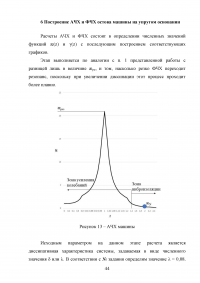
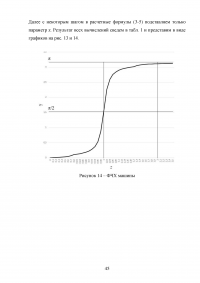
6 Построение АЧХ и ФЧХ остова машины на упругом основании
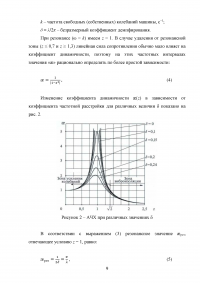
Расчеты АЧХ и ФЧХ состоят в определении численных значений функций æ(z) и γ(z) с последующим построением соответствующих графиков.
Этап выполняется по аналогии с п. 1 представленной работы с разницей лишь в величине æрез и том, насколько резко ФЧХ переходит резонанс, поскольку при увеличении диссипации этот процесс проходит более плавно.
...
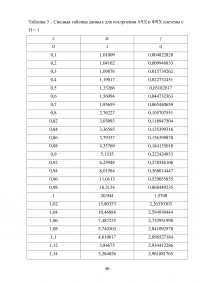
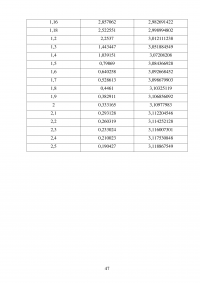
Таблица 3 – Сводная таблица данных для построения АЧХ и ФЧХ системы с Н = 1
...
ЗАКЛЮЧЕНИЕ
В курсовой работе выполнены следующие этапы расчета колебаний привода машины:
1) Составлены ДМ и ММ привода машины;
2) Определено значение собственной частоты крутильных колебаний;
3) Рассчитана амплитуда вынужденных крутильных колебаний при заданной частоте вынуждающей силы;
...