| Код | 418581 | ||
| Дата создания | 2020 | ||
| Страниц | 33 ( 14 шрифт, полуторный интервал ) | ||
| Источников | 12 | ||
| Изображений | 17 | ||
|
Файлы
|
|||
|
Без ожидания: файлы доступны для скачивания сразу после оплаты.
Ручная проверка: файлы открываются и полностью соответствуют описанию. Документ оформлен в соответствии с требованиями ГОСТ.
|
|||
Графическое представление функций позволяет приближённо решить любое уравнение с одним неизвестным и систему двух уравнений с двумя неизвестными.
Графическая иллюстрация часто помогает дать некоторые качественные ответы, найти число корней, указать отрезки на числовой оси, где они могут находиться.
Наглядность, свойственная графическому методу, при решении неравенств еще более ценна, чем при решении уравнений. Способы решения остаются теми же, а сами же решения в отличие от решений уравнений, чаще изображаются на графике не только отдельными точками, но и целыми участками числовой оси.
Основная ценность графического подхода к решению неравенств состоит в том, что уже схематическое изображение графика функций часто показывает, что неравенство выполняется в интервалах, ограниченных такими характерными точками, как точки пересечения графиков у = f1(x) и у = f2(x) между собой (или точки пересечения графика y = f(x) с осью Ох). Отыскание этих точек является уже несколько более легкой задачей: оно сводится к решению уравнений, а не неравенств.
В данной работе будут изложены основные методы решения линейных неравенств, применительно к конкретным задачам.
Объект данного исследования – процесс решения уравнений и неравенств.
Предмет - графический метод решения уравнений и неравенств.
1.1 Определения и понятия
Графический метод решения задачи линейного программирования основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.
...
1.2 Решение неравенств
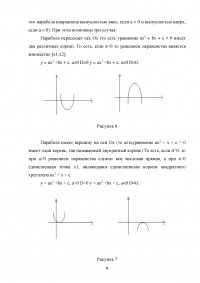
Если неравенство записано в виде f (x) > 0, то, построив график функции y=f (x), можно непосредственно по чертежу видеть, для каких значений х неравенство удовлетворяется (график лежит выше оси Ох). Решение будет точным или приближенным в зависимости от того, точно или приближенно найдены точки, где график переходит из нижней полуплоскости y < 0 в верхнюю полуплоскость y > 0.
...
2.1 Графический метод решения уравнений и неравенств, содержащих переменную под знаком модуля
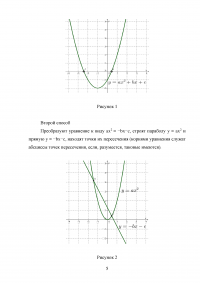
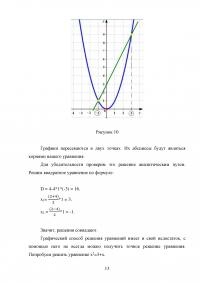
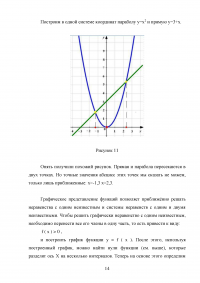
В основе графического метода лежит нахождение точек пересечения графиков функций левой и правой частей уравнения. Обычно данный метод применяется, когда графики обеих частей уравнения достаточно просто строятся и легко находятся точки пересечения этих графиков.
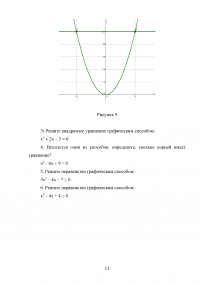
Одним из способов решения уравнений является графический способ. Он основан на построении графиков функции и определения точек их пересечения. Рассмотрим графический способ решения квадратного уравнения ax2+bx+c=0.
...
2.3 Функционально-графический метод решения уравнений с параметрами
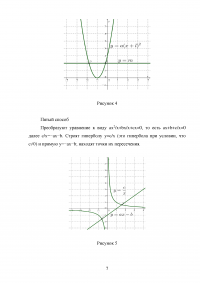
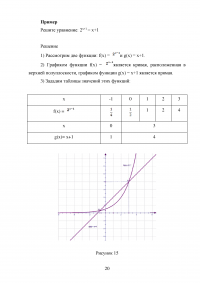
Задачи с параметрами, связанные с разрешимостью и числом решений уравнений и неравенств, наиболее удобно решать графическим методом.
Пусть уравнение относительно неизвестного х, содержащее параметр а, с помощью элементарных действий приводится к виду
...
ЗАКЛЮЧЕНИЕ
Не всякое уравнение или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению (неравенству) того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать другие методы решения, и одним из таких методов является графический метод решения уравнений и неравенств, которые мы рассмотрели.
...
ПРИЛОЖЕНИЕ А
Контрольная работа по теме квадратные уравнения и неравенства
...
ПРИЛОЖЕНИЕ Б
Контрольная работа по теме показательные и логарифмические уравнения и неравенства
...