Оптимизация модели синхронного инвестиционно-финансового планирования (однопериодная модель Дина)
| Код | 402541 | ||
| Дата создания | 2020 | ||
| Страниц | 27 ( 14 шрифт, полуторный интервал ) | ||
| Источников | 10 | ||
|
Файлы
|
|||
|
Без ожидания: файлы доступны для скачивания сразу после оплаты.
Ручная проверка: файлы открываются и полностью соответствуют описанию. Документ оформлен в соответствии с требованиями ГОСТ.
|
|||
Образцы страниц развернуть (27)
Содержание
Введение
Научный подход к принятию решений в значительной мере обусловлен развитием методов экономико-математического моделирования и применением в управлении фирмами электронно-вычислительной техники. При наличии множества вариантов решений в каждой конкретной ситуации экономико-математические модели позволяют без перебора всех возможных вариантов находить при заданных условиях самый лучший, то есть оптимальный вариант. Компьютеры, в свою очередь, ускоряют вычислительный процесс, быстро производят все необходимые преобразования экономической информации и выполняют такие расчеты, которые вручную произвести очень сложно.
Развитие информационных технологий и экономико-математических методов анализа проблемных ситуаций и принятия решений при грамотном их использовании способствуют совершенствованию внутрифирменного управления маркетингом, снабжением, производством, финансами, сбытом товара и другими управляющими подсистемами фирмы, существенно повышая эффективность управленческой деятельности.
Планирование, как центральное звено управления, охватывает систему принципов, методов, форм и приемов регулирования рыночного механизма в области использования ограниченных ресурсов с целью повышения конкурентоспособности хозяйственного субъекта. Сущность планирования в условиях рыночной экономики заключается в научном обосновании на предприятиях предстоящих экономических целей их развития и форм хозяйственной деятельности, выбора наилучших способов их осуществления, на основе наиболее полного выявления требуемых рынком видов, объемов и сроков выпуска товаров, выполнения работ и оказания услуг и установления таких показателей их производства, распределения и потребления, которые при полном использовании ограниченных производственных ресурсов могут привести к достижению прогнозируемых в будущем качественных и количественных результатов.
Оптимизационныезадачирешаются посредство выполнения соответствующих моделей с помощью методов математического программирования. [2]
Практическая реализация любой оптимизационной задачи осуществляется в результате выполнения следующих основных этапов:
1) Формулирование экономической постановки.
Определяются исходные посылки, основные условия, критерии оптимальности и искомые переменные.
2) Разработка экономико-математической модели (этап формализации).
На данном этапе создается система ограничений, математически описывающая основные условия решения задачи, а также содержащая наиболее целесообразный критерий оптимальности.
Критерий оптимальности – это выбранный на научной основе и предназначенный для характеристики конечного результата решения задачи показатель, экстремальное значение которого отражает предельно достижимую эффективность.
3) Разработка наиболее эффективного математического метода реализации модели.
В данной курсовой работе мы более подробно рассмотрим теоретические и методологические аспекты оптимизационного анализа, его основные понятия, методы оптимизации однопериодной модели Дина.
Целью данной курсовой работы является ознакомление с теоретическими аспектами процесса оптимизации модели синхронного инвестиционно-финансового планирования (однопериодной модели Дина) и использование полученных знаний на практике путем решения задач: на расчет оптимальной программы синхронного инвестиционного и финансового планирования для случая, когда инвестиционные проекты являются делимыми графическим методом и с помощью механизма поиска решений, поиск оптимальной программы синхронного инвестиционного планирования для случая неделимости инвестиционных объектов способом переборки и с помощью механизма поиска решения.
Фрагмент работы для ознакомления
1.1 Основные понятия оптимизационного анализа
Все существующие модели могут быть условно разделены на два класса - модели материальные, т.е. объективно существующие (которые можно "потрогать руками"), и модели абстрактные, существующие в сознании человека. Одним из подклассов абстрактных моделей являются модели математические. Предметом данного изучения будут математические модели, применяемые для анализа различных явления и процессов, имеющих экономическую природу. Применение математических методов существенно расширяет возможности экономического анализа, позволяет сформулировать новые постановки экономических задач, повышает качество принимаемых управленческих решений.
Математические модели экономики, отражая с помощью математических соотношений основные свойства экономических процессов и явлений, представляют собой эффективный инструмент исследования сложных экономических проблем. Математические модели экономических процессов и явлений называют экономико-математическими моделями (ЭММ).
...
1.2 Математическая постановка задач линейного программирования
Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.
Линейное программирование - наиболее разработанный и широко применяемый раздел математического программирования. Круг задач, решаемых при помощи методов линейного программирования достаточно широк:
...
2.1 Назначение и применение однопериодной модели Дина
Простейшую модель синхронного инвестиционно-финансового планирования создал американский экономист Д. Дин. В ней предполагается, что все объекты инвестирования функционируют только один период и к концу этого периода нужно полностью рассчитаться по всем кредитам. Предполагается также, что все инвестиционные проекты и источники их финансирования можно реализовать не в полном объеме и независимо друг от друга. При таких условиях из m инвестиционных проектов и n источников их финансирования нужно составить инвестиционно-финансовую программу, обеспечивающую максимальные чистые поступления в конце периода.
Для данной модели характерны следующие допущения:
...
3.1 Исходные данные для построения модели
Наша задача будет заключаться в том, чтобы:
1. Рассчитать оптимальную программу синхронного инвестиционного и финансового планирования для случая, когда инвестиционные проекты являются делимыми графическим методом и с помощью механизма поиска решений;
...
Таблица 1 - Исходные данные
...
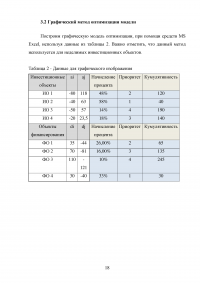
3.2 Графический метод оптимизации модели
Построим графическую модель оптимизации, при помощи средств MS Excel, используя данные из таблицы 2. Важно отметить, что данный метод используется для неделимых инвестиционных объектов.
...
Таблица 2 - Данные для графического изображения
...
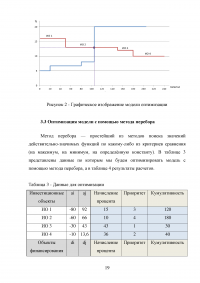
3.3 Оптимизация модели с помощью метода перебора
Таблица 3 - Данные для оптимизации
...
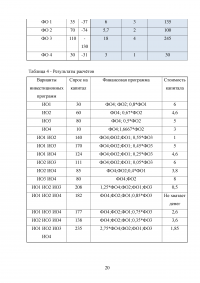
Таблица 4 - Результаты расчётов
...
3.4 Оптимизация модели Дина средствами MS Excel
Таблица 5 - Отчет о результатах при ограничениях Х€[0;1] и У€[0;1]
...
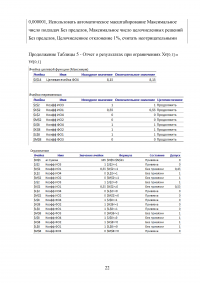
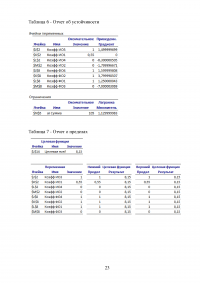
Таблица 6 - Отчет об устойчивости
...
Таблица 7 - Отчет о пределах
...
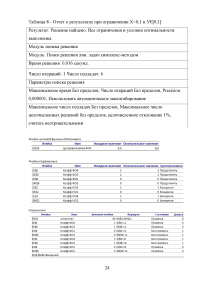
Таблица 8 - Отчет о результатах при ограничении Х=0;1 и У€[0;1]
...
ЗАКЛЮЧЕНИЕ
Человеку практически ежедневно приходится сталкиваться с проблемой принятия решений для достижения тех или иных целей. В экономике целями могут быть увеличение прибыли, снижение затрат, повышение производительности труда, рациональное использование оборудования и материалов, повышение эффективности инвестиций и многое другое. Для решения таких задач очень широко используется метод оптимизационного моделирования.
...
Список литературы [ всего 10]
- Методы принятия инвестиционно-финансовых программных решений в условиях определенности // Учебное пособие, Издательство Политехнического университета, 2015
- Л.С. Тарасевич, П.И. Гребенников, А. И. Леусский Теория корпоративных финансов // Учебник Санкт-Петербургский государственный университет экономики и финансов (Финек), 2014
- Экономико-математические методы и модели // Учебное пособие Екатеринбург, 2013
- Электронный ресурс «Постановка задач линейного программирования и их решение с помощью MS Excel» // Научный электронный архив», [режим доступа] http://econf.rae.ru/article/5667
- ...