| Код | 323210 | ||
| Дата создания | 2016 | ||
| Страниц | 34 ( 14 шрифт, полуторный интервал ) | ||
| Источников | 5 | ||
| Оригинальность | 64.3 % | Antiplagiat [ проверено 21.02.2022 ] | ||
|
Файлы
|
|||
|
Без ожидания: файлы доступны для скачивания сразу после оплаты.
Ручная проверка: файлы открываются и полностью соответствуют описанию. Документ оформлен в соответствии с требованиями ГОСТ.
|
|||
Файл работы содержит:
Цифровая обработка сигналов широко вошла в нашу жизнь с использованием DVD, модемов, мобильных телефонов. Широко используемым аппаратом для анализа и синтеза сигналов, как непрерывных, так и дискретных, является преобразование Фурье. Анализ сигналов предназначен для сравнения сигналов друг с другом, определения их сходства и различия для определения методов преобразования (например, с целью сжатия или модуляции). Однако преобразование Фурье оперирует комплексными числами, что значительно замедляет вычисление коэффициентов разложения и увеличивает область памяти, необходимую для хранения сигнала. От этих недостатков избавлено вейвлет- преобразование, которое является очень простыми операциями над действительными числами.
Вейвлеты (wavelets) – это обобщенное название временных функций, имеющих вид волновых пакетов. Вейвлеты создаются с помощью специальных базовых функций, задающих их тип и свойства. Они имеют явное преимущество перед рядами Фурье в представлении локальных особенностей функций. Благодаря этой особенности вейвлеты нашли практическое применение для анализа тонких особенностей сигналов и изображений, для их сжатия и очистки от шума.
Вейвлеты были предложены в 1990-х годах, хотя первый вейвлет Хаара был описан еще в 1909 г. Наибольший вклад в теоретическую разработку вейвлетов внесли Мейер, Добеши, Малл.
В настоящее время существует множество компьютерных систем, позволяющих проводить сложные математические расчеты, в том числе обработку сигналов и изображений. К таким системам относятся Mathcad, MatLab, Maple, Mathematica. Однй из самых популярных систем является Mathcad (MATHematica and Computer Aided Design), имеющая наиболее простой интерфейс в виде написания формул на листе бумаги, а не ввода определенных команд в командную строку.
Целью данного курсового проекта является исследование и реализация анализа сигналов с использованием вейвлет-преобразования в системе Mathcad:
1.1 Основы вейвлет-преобразования
Каждый сигнал представляет собой физический процесс, который передает сообщение. Любой непрерывный сигнал может быть заменен дискретными отсчетами - взятыми значениями сигнала через определенные промежутки времени.
Рассмотрим сигнал, состоящий из двух точек {x1, x2}. Эти значения могут быть заменены полусуммой и полуразностью:
...
1.2 Вейвлет-преобразование Хаара
ВП одномерного сигнала – это его представление в виде обобщенного ряда Фурье по системе базисных функций, локализованных как в пространственной, так и в частотной областях. Примером такой базисной функции может служить вейвлет Хаара, который определяется выражением прямоугольного импульса
...
1.3 Ортогональные вейвлеты Хаара и Добеши
Свойство ортогональности функций заключается в следующем: интеграл от произведения этих функций равен нулю, т.е. в переводе к векторному пространству это означает, что векторы перпендикулярны. Ортогональные вейвлеты используют в качестве базиса ортогональные функции. Главнее свойства этих вейвлетов- возможность восстановления не только локальных особенностей сигнала s(t), но и сигнала в целом.
Функция Хаара – простейший пример ортогонального вейвлета. Функция φ у него имеет значение 1 в интервале [0,1] и 0 за пределами этого интервала. Функция ψ имеет вид прямоугольных импульсов – меандра (значение 1 в интервале [0,0.5] и -1 в интервале [0.5,1]). Вейвлета Хаара хорошо локализованы в пространстве, но плохо локализованы в частотной области, поскольку меандр имеет широкий спектр частот (практически бесконечный).
...
2.1 Назначение пакета Mathcad
Mathcad является широко известным математическим пакетом с удобным интерфейсом. Mathcad представляет собой инженерную среду в виде электронной доски. В отличие от электронных таблиц интерфейс Mathcad принимает от пользователя через клавиатуру или мышь и отображает на дисплее естественную математическую нотацию. Для расширения возможностей Mathcad по отдельным научным дисциплинам Mathcad содержит четыре пакета расширений. Для данного курсового проекта наиболее важным является Wavelet Extension Pack, который позволяет анализировать сигналы и изображения, проводить статистическую оценку сигнала и анализ сжатия данных.
...
3 Применение вейвлетов для очистки сигналов от шума
Для удаления шутов используется известный прием: удаление высокочастотных составляющих из спектра сигнала. Используя вейвлет- спектр сигнала, можно удалить шумы, ограничивая уровни детализирующих коэффициентов.
Шумы относят к кратковременным особенностям сигнала. Они создают детализирующие коэффициенты с высоким содержанием шумовых компонент. Уменьшить уровень шумов можно, если задать некоторый порог для их уровня и срезать по уровню детализирующие коэффициенты. Уровень ограничения можно устанавливать для каждого коэффициента отдельно с помощью фильтров. Это позволяет строить адаптивные к изменениям сигнала системы очистки от шумов на основе вейвлета.
Удаление шума с использованием ортогональных вейвлетов включает в себя следующие действия:
...
4 Применение вейвлетов для сжатия изображений
Простейшим видом вейвлет-базиса для изображений является разделимый базис, получаемый сжатием и растяжением одномерных вейвлетов. Для изображения будем использовать двумерное вейвлет преобразование- отдельно по строкам и столбцам.
Для построения разделимого базиса на каждом шаге преобразования выполняется два разбиения по частоте, а не одно. (т.н. двумерные вейвлеты). Предположим, имеем изображение размером N-N. Сначала каждая из N строк изображения делится на низкочастотную и высокочастотную половины.
...
ЗАКЛЮЧЕНИЕ
В данном курсовом проекте отражено применение вейвлет- преобразования для удаления шутом и сжатия сигналов. Преобразования проводились в системе Mathcad с использованием пакета расширения Wavelet Extension.
Для удаления шумов использовались два способа: одномерное вейвлет – преобразование и одномерный кратномасштабный анализ. В обоих случаях результаты удаления шума достаточно хорошие – получили исходный сигнал без шума - синусоиду. Качество очистки зависит от количества уровней вейвлет- разложения и количества удаленных коэффициентов. Однако для более сложных сигналов нужно найти баланс между шумовыми составляющими и высокочастотными особенностями сигнала.
...
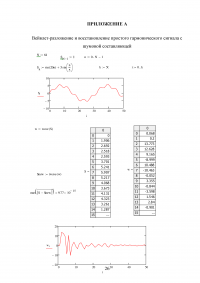
ПРИЛОЖЕНИЕ А
Вейвлет-разложение и восстановление простого гармонического сигнала с шумовой составляющей
...
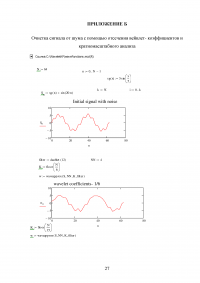
ПРИЛОЖЕНИЕ Б
Очистка сигнала от шума с помощью отсечения вейвлет- коэффициентов и кратномасштабного анализа
...
ПРИЛОЖЕНИЕ В
Сжатие изображение с помощью отсечения вейвлет-коэффициентов
...
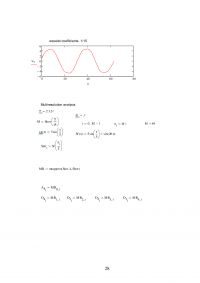
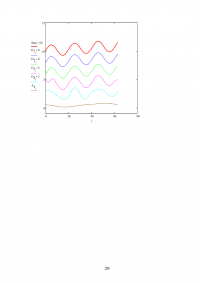
ПРИЛОЖЕНИЕ Г
Нестандартные функции вейвлет-преобразования из пакета Wavelet Extension
...