Методика изучения тригонометрических неравенств
| Код | 296379 | ||
| Дата создания | 2018 | ||
| Страниц | 36 ( 14 шрифт, полуторный интервал ) | ||
| Источников | 30 | ||
|
Файлы
|
|||
|
Без ожидания: файлы доступны для скачивания сразу после оплаты.
Ручная проверка: файлы открываются и полностью соответствуют описанию. Документ оформлен в соответствии с требованиями ГОСТ.
|
|||
Образцы страниц развернуть (36)
Содержание
Введение
Тригонометрические неравенства занимают одно из главных мест в курсе математики средней школы, как по содержанию учебного материала, так и по способам учебно-познавательной деятельности, которые могут и должны быть сформированы при их изучении и применены к решению огромного количества задач.
В школьном курсе математике с изучением тригонометрических неравенств связаны такие направления:
- решение неравенств;
- решение систем неравенств;
- доказательство неравенств.
Рассматривая научно-методической литературу, видим, что много внимания обращено к первому и второму направлениям.
Еще обратим внимание, что решение тригонометрических неравенств создаёт предпосылки для систематизации знаний учащихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, способы преобразования тригонометрических выражений и т.д.) и даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.). [1]
Актуальность исследования: анализ материала по изучению тригонометрических неравенств в разнообразных учебных пособиях «Алгебра и начала анализа» различных авторов, говорит о том, что перед преподавателем стоит задача – формировать у учащихся умения решать неравенства любого вида, развивая тем самым общие тригонометрические представления.
Цель данной работы: Разработать методику изучения тригонометрических неравенств.
Объект данной работы: процесс обучения математике.
Предмет данной работы: методика изучения тригонометрических неравенств.
Задачи:
- провести анализ психолого-педагогической, учебной и методической литературы по теме работы;
- выявить роль тригонометрических неравенств в изучении математики;
- выделить основы формирования умений необходимых для решения тригонометрических неравенств;
- классифицировать способы решения тригонометрических неравенств;
- разработать методику формирования умений и навыков решать тригонометрические уравнения и неравенства.
Данная работа состоит из введения, 4 пунктов с подпунктами, заключения и списка литературы, включающего 30 источников, приложения, в котором представлен конспект урока.
Фрагмент работы для ознакомления
1 История развития тригонометрии
Тригонометрия возникла еще в древности. Ее возникновение тесно связано с земледелием, астрономией и строительным делом. Огромен вклад в развитие тригонометрии Л. Эйлера, он создал тригонометрию как науку о функциях, дал ей аналитическое изложение, вывел всю совокупность формул из немногих основных формул. Обозначать стороны малыми буквами и противолежащие углы — соответствующими большими буквами упростило все формулы, внесло в них ясность и стройность. Эйлеру принадлежит мысль смотреть на тригонометрические функции как на отношения соответствующих линий к радиусу круга, т. е. как числа, причём радиус круга как «полный синус» он взял за единицу. Эйлер получил много новых соотношений, установил связь между тригонометрическими и показательными функциями, ввел правило знаков функций для всех четвертей, вывел обобщённую формулу приведения, нашел в тригонометрии много ошибок, которые допускались, можно сказать, во всех европейских учебниках математики.
...
2 Анализ учебников
Рассмотрим учебники «Алгебра и начала анализа. 10-11» Мордковича А.Г. и Колмогорова А.Н.
В учебнике Мордковича А.Г. 8 глав. В конце каждой главы выделены основные результаты данной главы. Курс математики в 10 классе начинается с первой главы «Тригонометрические функции». Здесь автор рассматривает понятие тригонометрической окружности на координатной плоскости, определения синуса и косинуса, основные тригонометрические соотношения, связанные с ними, показывает решения простейших тригонометрических уравнений по окружности. Знакомство с формулами приведения происходит только после изучения тригонометрических функций углового аргумента. Затем изучаются свойства и графики тригонометрических функций. В следующей главе «Тригонометрические уравнения» детально показано решение каждого простейшего тригонометрического уравнения, на базе ранее введенных определений арксинуса, арккосинуса, арктангенса. Тут же показаны такие способы решения, как разложение на множители и введение новой переменной; метод решения однородных тригонометрических уравнений. Другие способы решения показаны только после изучения третьей главы «Преобразование тригонометрических выражений».
Схема изучения показана следующим образом: функция → уравнения → преобразования.
...
3.1 Решение простейших тригонометрических неравенств
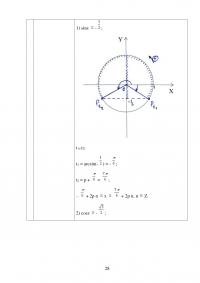
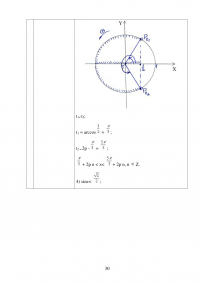
Большинство авторов в современных учебниках алгебры и начала анализа предлагают начинать данную тему с решения простейших тригонометрических неравенств. Алгоритм решения простейших тригонометрических неравенств основан на знаниях и умениях определять на тригонометрической окружности значения не только основных, но и различных тригонометрических углов.
...
3.2 Метод интервалов
Многолетний опыт учителей математики показывает, что учащиеся, хорошо решающие тригонометрические уравнения, часто испытывают большие сложности при решении тригонометрических неравенств, делая большое количество ошибок в окончательном отборе решений, после того как сделана основная часть работы. Ошибки появляются от невнимательности или когда учащиеся не до конца поняли каких-либо специфических особенностей неравенства. Нет помощи и от проверки. Она бывает достаточна, для того чтобы найти ошибку. Также если в ответе один-два интервала проверка утомительна, а при наличии нескольких интервалов техническая сложность проверки очень сильно возрастает.
Из-за этого разработан особый методический подход к последнему этапу решения тригонометрического неравенства, который удобно показать учащимся с помощью специального алгоритма.
1) Привести неравенство к виду, когда в одной из его частей (например, в правой) был ноль.
...
4 Методика изучения тригонометрических неравенств
Целью подготовительного этапа является необходимость сформировать у школьников умения использовать тригонометрическую окружность или график для решения неравенств, а именно:
...
ЗАКЛЮЧЕНИЕ
Изучив психолого-педагогическую и методическую литературу по данной теме, стало ясно, что умение и навыки решать тригонометрические неравенства в школьном курсе алгебры и начал анализа являются очень важными и их развитие требует достаточно больших усилий со стороны учителя математики.
...
ПРИЛОЖЕНИЕ
Конспект урока алгебры в 10-м классе по теме: «Решение тригонометрических неравенств».
(по учебнику алгебры и начала анализа Мордковича А.Г.)
Задача урока: закрепление умений и навыков решения простейших тригонометрических неравенств, в которых содержатся функции синус и косинус, научится решать более сложные неравенства.
Цели урока:
- Запоминание тригонометрических формул, табличных значений тригонометрических функций, формул корней тригонометрических уравнений;
...
Список литературы [ всего 30]
- Аджиева А. Тригонометрические уравнения // Математика. Приложение к газете «Первое сентября» № 33, 2001г.
- Адрова И.А., Ромашко И.В. Модульный урок в X классе по теме «Решение тригонометрических уравнений» //Математика в школе. 2001. №4. С. 28-32.
- Арлазаров В. В., Татаринцев А. В., Тиханина И. Г., Чекалкин Н. С. Лекции по математике для физико-математических школ. Часть 2. ЛКИ, 2008, С. 264.
- БашмаковМ.И. Алгебра и начала анализа. 10-11. Учебное пособие для 10 – 11 кл. средней школы. М. Просвещение, 1998. – 335 с.: ил.
- Водинчар М.И. и др. Метод концентрических окружностей для систем тригонометрических неравенств //Математика в школе. 1999. № 4. С. 73-77.
- ...