| Код | 277184 | ||
| Дата создания | 2014 | ||
| Страниц | 12 ( 14 шрифт, полуторный интервал ) | ||
|
Файлы
|
|||
|
Без ожидания: файлы доступны для скачивания сразу после оплаты.
Ручная проверка: файлы открываются и полностью соответствуют описанию.
|
|||
1. Комбинаторика
Сколько существует способов распределения трех первых мест при восьми командах, участвующих в соревнованиях?
2. Элементарная теория вероятностей
Из совокупности всех подмножеств множества S = {1, 2, …, N}по схеме выбора с возвращением выбираются А1, А2. Найти вероятность того, что А1 ∩ А2 = Ǿ.
3. Распределения вероятностей, условная вероятность
В партии из 200 изделий каждое изделие независимо от остальных может быть бракованным с вероятностью 0,01. Оценить вероятность того, что число бракованных изделий в этой партии больше двух.
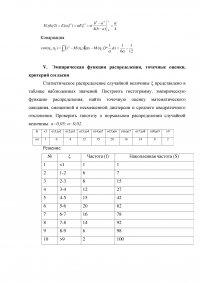
4. Математическое ожидание и дисперсия
Случайная величина ξ имеет равномерное распределение на отрезке [0;1]. Найти математические ожидания, дисперсии и корреляцию случайных величин: η1 = ξ²; η2 = αξ .
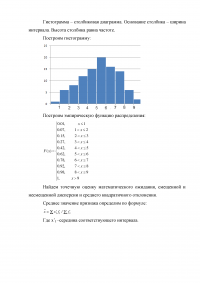
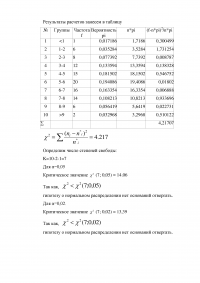
5. Эмпирическая функция распределения, точечные оценки, критерий согласия
Статистическое распределение случайной величины ξ представлено в таблице наблюденных значений. Построить гистограмму, эмпирическую функцию распределения, найти точечную оценку математического ожидания, смещенной и несмещенной дисперсии и среднего квадратичного отклонения. Проверить гипотезу о нормальном распределении случайной величины: α=0,05; α=0,02.
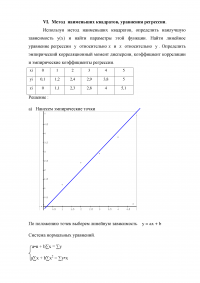
6. Метод наименьших квадратов, уравнения регрессии.
Используя метод наименьших квадратов, определить наилучшую зависимость y(x) и найти параметры этой функции. Найти линейное уравнение регрессии y относительно z и z относительно y . Определить эмпирический корреляционный момент дисперсии, коэффициент корреляции и эмпирические коэффициенты регрессии.