Особые точки функций комплексного переменного и их изучение с помощью WinMaple
| Код | 100915 | ||
| Дата создания | 2016 | ||
| Страниц | 50 ( 14 шрифт, полуторный интервал ) | ||
| Источников | 23 | ||
| Оригинальность | 62.3 % | Antiplagiat [ проверено 03.04.2024 ] | ||
|
Файлы
|
|||
|
Без ожидания: файлы доступны для скачивания сразу после оплаты.
Ручная проверка: файлы открываются и полностью соответствуют описанию. Документ оформлен в соответствии с требованиями ГОСТ.
|
|||
Образцы страниц развернуть (50)
Содержание
Введение
По определению, которое было предложено В.П. Дьяконовым – системы компьютерной математики (СКМ) – это программные средства, с помощью которых можно автоматизировать выполнение как численных, так и аналитических (символьных) вычислений и расчетов [2].
Первые СКМ появились на рынке программных средств в 60-х годах ХХ века. Самое бурное период их развития приходится на 90-е годы ХХ века. Современные СКМ оснащены удобным интерфейсом и мощным графическим инструментарием, в них реализовано значительное количество стандартных и специальных математических операций, функций и методов. Определяющими характеристиками современных СКМ является наличие собственных языков программирования, средств подготовки математических текстов к печати, обеспечение возможностей осуществлять импорт данных для использования других программных продуктов, в частности, электронных таблиц, и экспорт данных в них [1].
Каждая из СКМ имеет определенные нюансы в архитектуре, однако все они имеют типовую структуру, составляющими которой является вычислительное ядро системы, библиотеки процедур и функций, пакеты расширений, справочная система и интерфейс пользователя [2].
Одним из ярких представителей СКМ является программная среда WinMaple, которая характеризуется наилучшим, среди всех СКМ ядром символьных вычислений, высокой точностью вычислений, возможностью осуществления ввода математических соотношений в привычной нотации, структурированностью документов и удобностью интерфейса.
Результаты исследования показывают целесообразность использования СКМ и в частности WinMaple в качестве эффективного инструментального средства при изучении высшей математики в высших учебных заведениях, которое применяется практически во всех ведущих университетах мира.
Теория функций комплексной переменной (ТФКП) занимает одно из главных мест в курсе математики высшей школы. ТФКП имеет много практических применений [1, 2]. Методами ТФКП решают некоторые задачи картографии, теории упругости, гидро-, аэро - и электродинамики.
Функции комплексной переменной применяются для решения задач квантовой теории, в изучении движения небесных тел и во многих других отраслях науки и техники. Вместе с практическими применениями теория аналитических функций используется в решении теоретических проблем математики, в частности, в теории чисел. С помощью таких функций вычисляют сложные интегралы, решают дифференциальные уравнения и т.п.
Темой выпускной квалификационной работы является исследование возможности применения средств WinMaple для решения практических задач определения и изучения особых точек функций комплексного переменного в курсе высшей математики высшего учебного заведения.
Целью выпускной квалификационной работы является разработка методических рекомендаций для решения практических задач определения и изучения особых точек функций комплексного переменного в курсе высшей математики высшего учебного заведения.
Структурно работа состоит из 2-х глав, заключения и введения.
В введении расмотрены аспекты применения систем компьютерной математике в учебном процессе.
В первой главе работы рассмотрены вопросы, связанные с использованием WinMaple в качестве инструментального средства для получения компетенций студентами при изучении высшей математики, теоретические и практические аспекты определения и изучения особых точек функций комплексного переменного.
Во второй главе работы рассмотрены вопросы, связанные с разработкой методических рекомендаций для решения практических задач определения и изучения особых точек функций комплексного переменного в курсе высшей математики высшего учебного заведения.
В заключении работы сделаны общие выводы по работе по изучению темы, данны методические рекомендации по проведению занятий.
Фрагмент работы для ознакомления
1.1 Анализ возможностей WinMaple для применения решений практических задач в курсе «Высшей математики»
Как правило, СКМ, и в том числе WinMaple, используют для решения научных, инженерных, учебных задач, наглядной визуализации данных и результатов вычислений и как удобные и полные справочники по математическим вычислениям. Вместе с тем, что благодаря мощной графике, средствам визуального программирования и использования мультимедиа технологий, роль СКМ выходит за рамки только математических расчетов. Они широко используются в образовании как мощные инструментальные средства для подготовки электронных занятий, курсов лекций и электронных книг с динамическими примерами
...
1.2.2 Нахождение особых точек и определение их типа у рациональных рядов
Пусть функция f(z) аналитическая в кольце 0 <|z — а| <ρ, но не аналитическая в точке а (a≠∞). Тогда точка а называется изолированной особой точкой однозначного характера для функции f(z).
В зависимости от поведения функции f(z) вблизи точки а различают три типа особых точек.
...
1.3.1 Определение нулей аналитических функций
Рассмотрим решение практического задания в среде WinMaple.
Найти все нули и их кратности функции f(z) = z sinh(z).
Решение
Опишем исходную функцию (рис.1.1):
...
1.3.3 Ряды Лорана
Рассмотрим выполнение следующего практического задания.
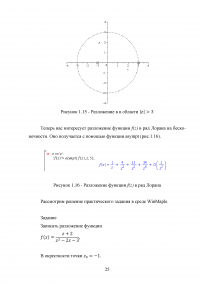
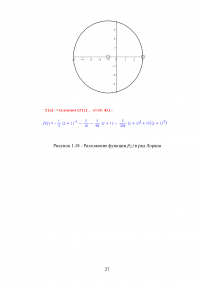
Рассмотреть различные разложения в ряд Лорана функции
f(z)=(z+2)/(z^2-2z-3),
Выбрав z_0=0.
Решение
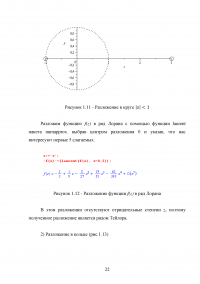
Выбор 0 в качестве z0, означает, что нужно получить разложение этой функции по степеням z. Функция f(z) имеет две особые точки: z = — 1 и z = 3,
...
2.1 Дидактический материал
Значение темы в курсе.
Изучение темы «Изучение особых точек комплексного переменного» в курсе "Высшей математики" для студентов Высших учебных заведений имеет большое значение, во-первых, это связано с тем, что изучаемые вопросы определены учебным планом дисциплины, а во-вторых являются достаточно важными с точки зрения предоставления обучаемым знаний о понятии комплексных переменных и работе с ними, свойствах, способах использования для решения других практических задач.
ТФКП занимает одно из главных мест в курсе математики высшей школы. ТФКП имеет много практических применений [1, 2]. Методами ТФКП решают некоторые задачи картографии, теории упругости, гидро-, аэро - и электродинамики.
...
Таблица 2.1 - Цели изучения темы «Изучение особых точек комплексного переменного» в рамках курса «Высшая математика»
...
2.2 Формы активизации познавательной деятельности и пути преодоления трудных мест
При чтении лекции, так как для студентов трудно в течение всего занятия внимательно слушать и писать, необходимо делать короткие паузы, заполняя их различными игровыми моментами, связанными с темой. Предлагать обращаться к электронному учебнику или Help системы Maple, и изучить часть по материалу при помощи электронного учебника.
Затем каждый получает индивидуальные задания, например, такие:
Найти все точки комплексной плоскости, в которых функция f (z) является дифференцированной. Найти производную в этих точках. Найти точки аналитичности данной функции.
...
2.3 Формирование предложений в перспективно-тематический план по высшей математике
Содержание курса высшей математики в высшем учебном заведении определяется типовой программой и созданными на кафедрах рабочими программами. Рабочие программы и планы учитывают не только общие обязательные положения курса высшей математики, но и ее прикладные аспектов ты, необходимые для глубокого изучения специальных дисциплин при подготовке бакалавров и магистров. Однако количество часов в курс высшей математики в учебных планах в настоящее время определяется без участия специалистов и поэтому не всегда обоснованно. Взаимный обмен рабочими программами и рабочими планами для родственных специальностей не всегда практикуется.
...
Таблица 2.2 - Предложения в Перспективно-тематический план по «Высшей математике»
...
ЗАКЛЮЧЕНИЕ
Содержание курса высшей математики в высшем учебном заведении определяется типовой программой и созданными на кафедрах рабочими программами. Рабочие программы и планы учитывают не только общие обязательные положения курса высшей математики, но и ее прикладные аспектов ты, необходимые для глубокого изучения специальных дисциплин при подготовке бакалавров и магистров. Однако количество часов в курс высшей математики в учебных планах в настоящее время определяется без участия специалистов и поэтому не всегда обоснованно.
Использование СКМ иллюстрирует возможности компьютера, позволяет акцентировать внимание на прикладных задачах, особенностях численного и символьного решения задач, выяснять границы применения компьютеров и математических методов, а также существенно повышают заинтересованность студентов в глубоком изучении математики, помогают усвоить структурные связи различных разделов курса. Деятельность преподавателя направляется на то, чтобы студент осознал, что при подготовке к инженерной деятельности без знаний по курсу высшей математики не может сформироваться специалист. Знания по математике относятся к фундаментальной системы знаний, на базе которой строится обучение студентов.
...
Список литературы [ всего 23]
- Лаврентьев М. А. Методы теории функций комплексного переменного / Лаврентьев М. А., Шабат Б. В. — М. : Наука, 1987. — 688 с.
- Радыгин В. М. Применение функций комплексного переменного в задачах физики и техники : учеб. пособие для пед. Вузов / Радыгин В. М., Голубева О. В. — М. : Высш. школа, 1983. — 160 с.
- Раков С. А. Компьютерные эксперименты в геометрии : учеб. пособие для учащихся по курсу геометрии / Раков С. А., Горох В. П. – Х. : РЦНИТ, 1996. –175 с.
- Клочко Т. В., Парфёнова Н. Д. Решение задач комплексного анализа средствами Maple / Клочко Т. В., Парфёнова Н. Д.. – ХНУ, 2009. – 69 c. (http://dspace.univer.kharkov.ua/handle/123456789/1390)
- Дьяконов В. П. Maple 9 в математике, физике и образовании / Дьяконов В. П. – М. : СОЛОН-Пресс, 2004. – 688 с.
- ...